9 Secrets about the Circle of Fifths
Everything you need to know about the circle of fifths in 12 minutes so you don’t fall behind in music class.
At the end of this episode, you will be able to fully understand the Circle of fifths: what it is, how it works, the relative minor, enharmonic keys and the logic behind the key signatures.
By following the next tips, you will easily reason out and memorize the circle of fifths.
Let’s break it down now!
What is the Circle of Fifths
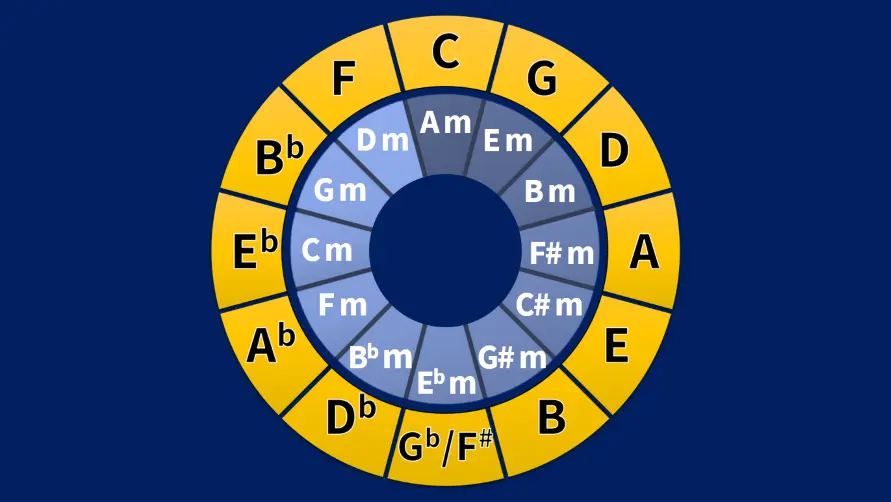
The Circle of fifths is a visual music tool that shows the relationships between the 12 notes of the Western classical music system.
Its shape reminds us of a clock or a pizza cut in 12 parts.
Each spot around the circle of fifths represents a note, a chord, and a major key.
How does the circle of fifths work?
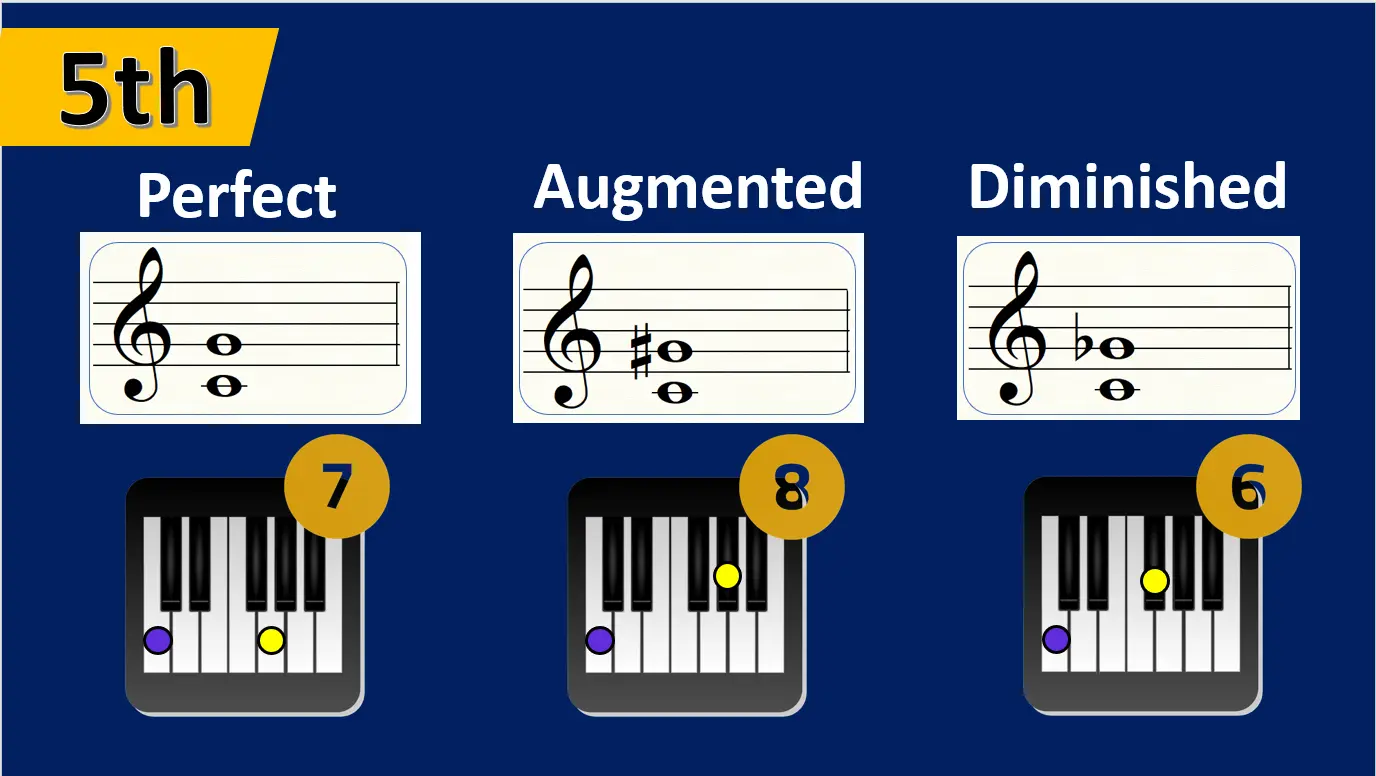
Before we start moving around the circle, we need to understand that a fifth is the distance between five consecutive notes.
There are three types of fifths depending on the number of semitones between the notes:
- Perfect fifths (7 semitones)
- Augmented fifths (8 semitones)
- Diminished fifths (6 semitones)
But, why does it matter?
Because in the circle of fifths, all the keys are going to be separated by perfect fifths or, in other words, that distance of 7 semitones.
For instance, if we move a perfect fifth up from C, we get to G. That is a distance of 7 semitones.
An if we move a perfect fifth down from C, we get to F. That is again 7 semitones but counting down.
Alright, let’s apply this to the actual circle of fifths!
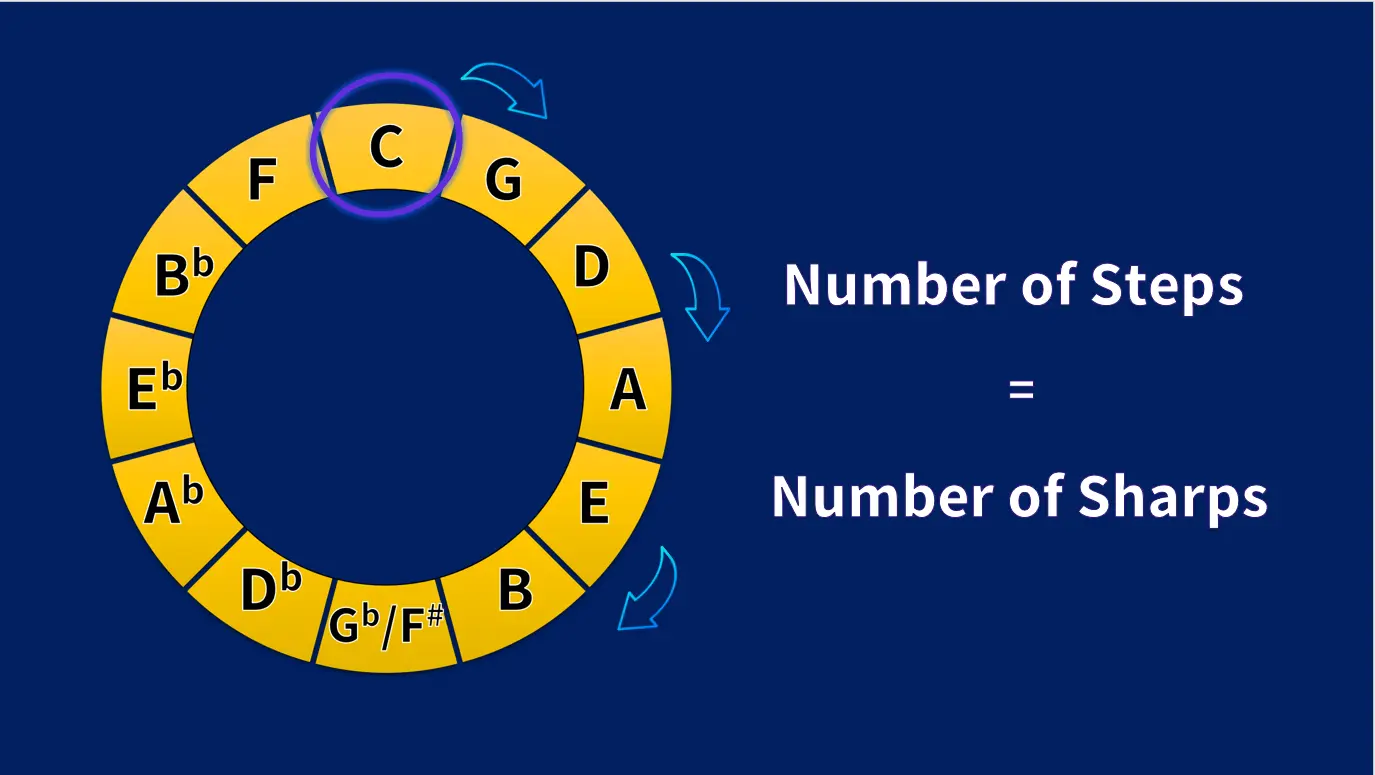
Moving clockwise: Keys with Sharps
Here our anchor point is C, at 12 o’clock.
Moving clockwise around the circle of fifths, we need to move up in perfect fifths.
Remember a perfect fifth is an interval of 7 semitones.
As we move clockwise, each key gains one sharp.
Making your life easier: the number of steps you take moving clockwise around the circle tells you how many sharps the key will have.
Let’s understand this better with an example.
Our starting point was C Major and we realize there are no sharps or flats in this key.
If we move one step clockwise, we get to G Major which has one sharp.
If we go a step further, this is two steps away from C Major, we get to D Major, which will have 2 sharps.
At this point, we can guess that, A Major will have 3 sharps, E Major will have 4 sharps, B Major; 5 and F# Major 6 sharps.
Moving Anticlockwise: Keys with Flats
Moving anticlockwise around the circle of fifths, we need to count down in perfect fifths.
As we move in this direction, each key gains one flat.
In other words: the number of steps you take moving anticlockwise around the circle tells you how many flats the key will have.
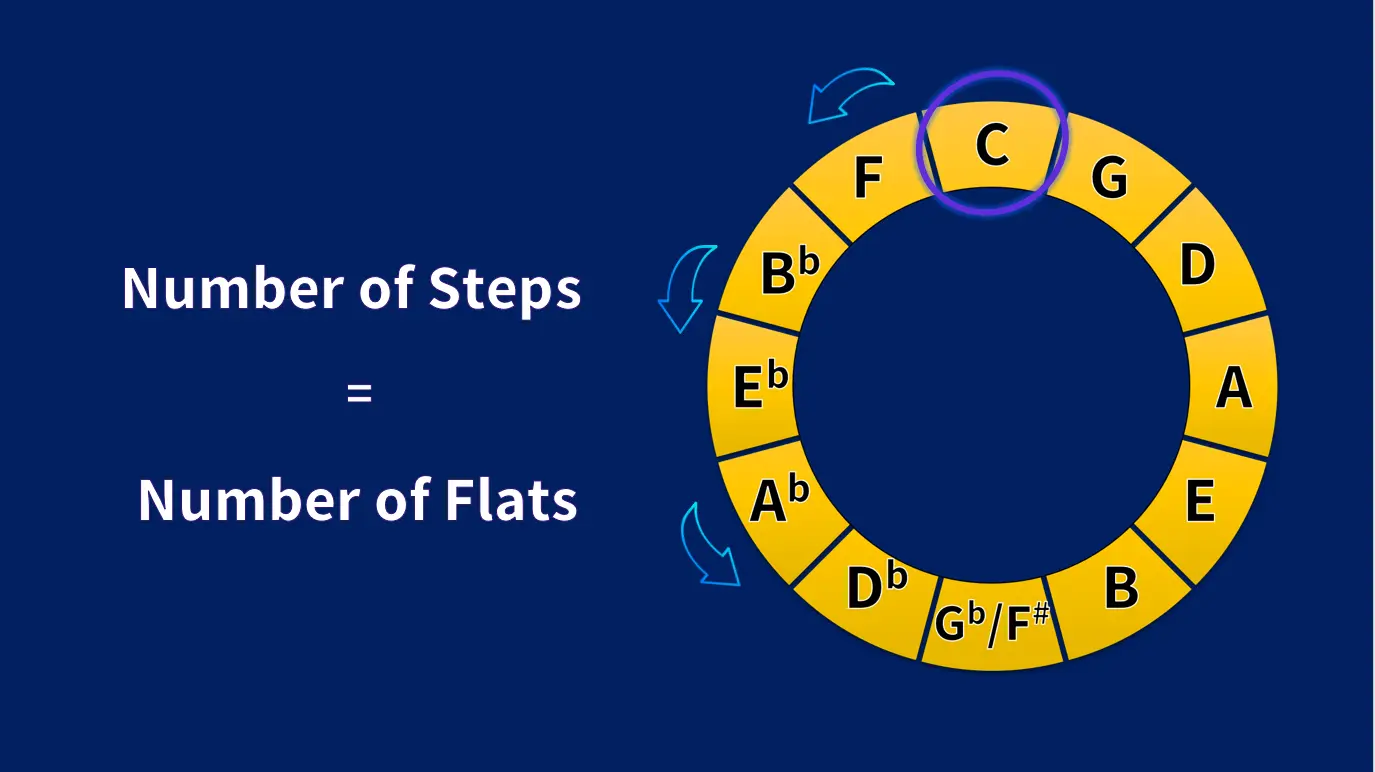
Here comes an example. Our starting point is still C.
If we move one step anticlockwise, we get to F Major which has one flat.
If we go a step further, this is two steps away from C, we get to Bb Major which will have 2 flats.
If we carry on, Eb Major will have 3 flats, Ab Major will have 4 flats; Db Major, 5 and Gb Major, 6 flats.
But careful with this common mistake: For some reason, many students confuse the key of Bb Major with B Major or the key Eb Major with E Major. We have to specify the word ‘flat’ is within the title of key with flats.
What is the Order of the Sharps?
Alright! That seems easy, you now know how to figure out the number of sharps and flats of any major key. But which are those sharps or flats exactly? And most importantly, in which order do they go?
Well, the good news is that sharps also follow the circle of fifths clockwise and they add up.
You just need to remember that the first sharp is F.
Then, to get more sharps, you need to move clockwise from F.
So, for the second sharp, we move clockwise along the circle and get C.
For a third sharp, move one step further to G. And so on!
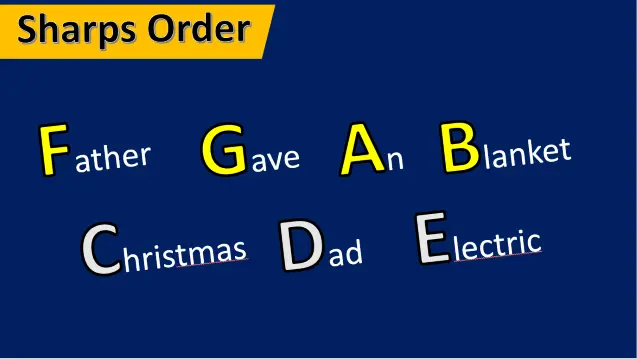
So, we notice that new sharps are added in the order F-C-G-D-A-E-B.
If you want to memorize anything of the circle of fifths, this sequence is definitely it!
You can use a mnemonic device to remember the order of the sharps, like:
Father-Christmas-Gave-Dad-An-Electric-Blanket.

Let’s see an example with real keys and key signatures:
When we were in G Major, we said we had one sharp. Now we know, it’s F# because F is the first sharp.
If we were in D Major and we said to have 2 sharps. We keep F as the first sharp and add up the next in the circle, C#.
What is the Order of the Flats?
Flats will follow the circle anticlockwise and will also add up;
The first flat will be Bb.
Then, to get more flats, you need to move anticlockwise from Bb.
So, for the second flat, we move anticlockwise along the circle and get Eb.
For a third flat, move one step further to Ab.
And so on!
So to get the order of flats all we have to do is reverse the order of the sharps.
B-E-A-D-G-C-F
Recall the order of the flats by saying:
Big Elephants Always Drive Go Cars Fast


Let’s put this into practice:
When we were in F Major, we said we had one flat. Now we know, the first flat is always Bb.
If we were in Bb Major and we said to have 2 flats. We keep B as the first flat and add up the next in the circle, Eb.
As we see, the addition of sharps and flats follows a pattern when going around the Circle of Fifths step by step. The direction you’re heading in tells you whether you’re adding sharps or flats.
Remember: no key signature has both sharps and flats.
Relative minor
Every major key has a relative minor key. This means that both keys share the same key signature.
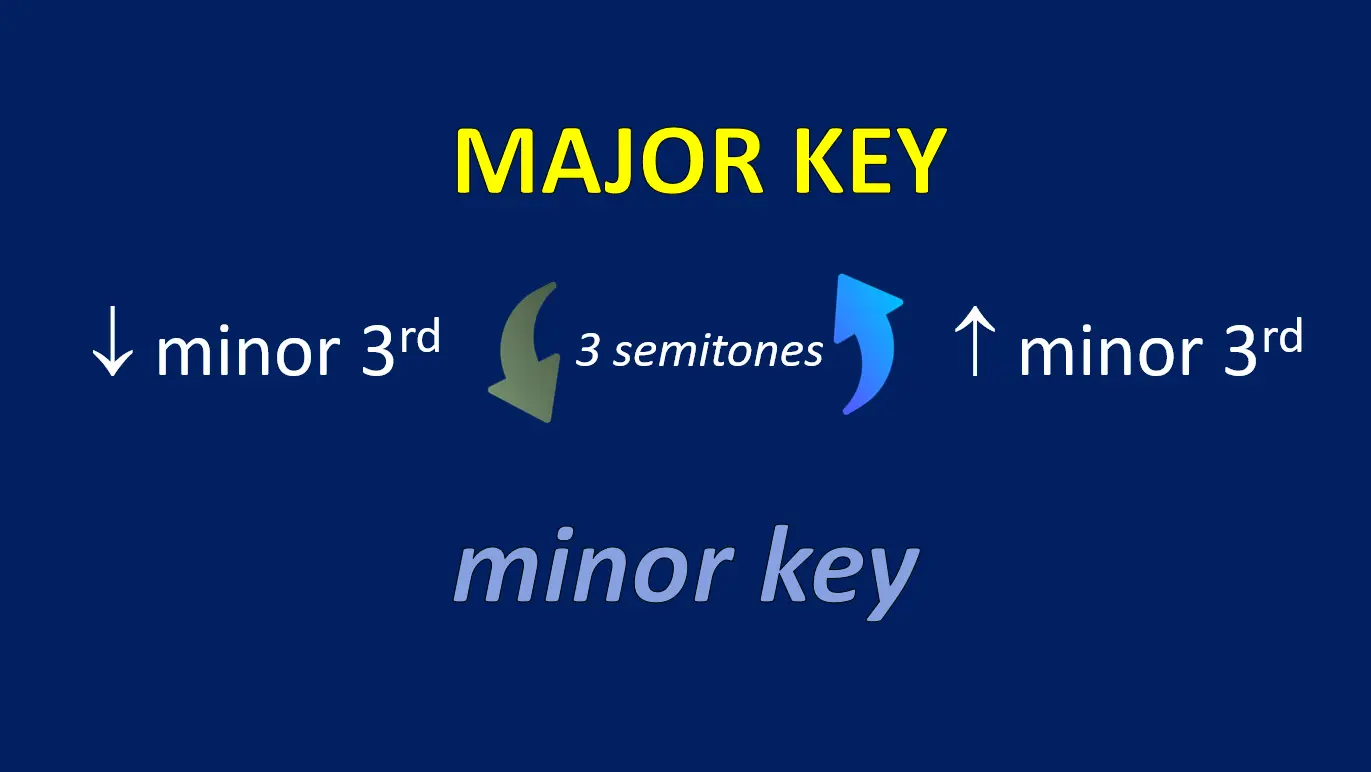
To find the relative minor of a major key, all you have to do is count a minor third (3 semitones) down from the mayor key.
If you need to find the relative major of a minor key, just reverse the process and count a minor third up from the minor key.
Let’s have a look at these examples.
C Major has no sharps or flats. Count down 3 semitones and find its relative minor, A minor.
Same with G Major, count down 3 semitones and get E minor as the relative.
If we continue with this process, we get an inner circle with all the minor keys.

How to find the Major key of a key signature
Now comes probably the most fun and most helpful side or the circle of fifths.
And that is figuring out the Major key of a given key signature.
Fear not! We will give you a couple of tricks to make this really easy!
Eventually, you will even find that you begin to memorize them and no longer need the shortcuts.
The trick to find the major key of a key signature with sharps is to look at the last sharp and raise it a semitone.

So if we have 3 sharps: F-C-G, we take the G#, raise it a semitone, and we get that our major key is A Major.
Let’s suppose we now have 5 sharps on the key signature. These are: F-C-G-D-A.
So, again, we would look at the last sharp, A#, raise it a semitone and get B as our Major key.
But careful! This trick won’t work for flats.
The shortcut to find the major key of a key signature with flats implies looking at the penultimate flat. That is going to give us the name of the major key we are in.

For instance, when we have 4 flats on a key signature: B-E-A-D, we look at the penultimate and get the key: Ab Major.
There is just one exception to this. In F Major, we only have one flat in the key signature, so there is no penultimate flat to look at.
To find out which key we are in, you can simply memorize the first flat is Bb or jump to the other end of the flats sequence to find it.
B E A D G C (F)
How to find the minor key of a key signature
Now, we know that every key signature can be shared by a major key and its relative minor.
Do you want the easiest way to find the minor key of a key signature?
Use the trick we just learnt and get the relative major key first.
Once you have it, just count down 3 semitones, as we said, and you will get the minor key of that key signature.
For instance, we had 3 sharps in A Major. Lower A 3 semitones and you get F#.
So, if we have 3 sharps in the key signature we may be in A Major or F# minor.

The same applies for keys with flats.
In F Major we had 1 flat. Now, lower that F, 3semitones and you get to the relative minor, D. So, with one flat on the key signature, we may be in F Major or D minor.
Enharmonic keys
At this stage, it is time to talk about the bottom of the circle of fifths.
We covered key signatures up to 5 sharps and flats. Let’s resume there!
Moving 5 spots clockwise from C gave us B Major having 5 sharps.
Jumping 5 spots anticlockwise from C took us to Db Major, with 5 flats.
Now if we keep moving on opposite directions, we would meet at the bottom of the circle.
Moving a perfect fifth (7 semitones) up from B would take us to F# Major, while moving a perfect fifth down from Db would take us to Gb Major.
Now, why are we stuck in the same place with two different names? Is the circle of fifths not working? Absolutely not!
F# Major and Gb Major are what we call enharmonic keys.
They are two keys that sound exactly the same but are written differently.
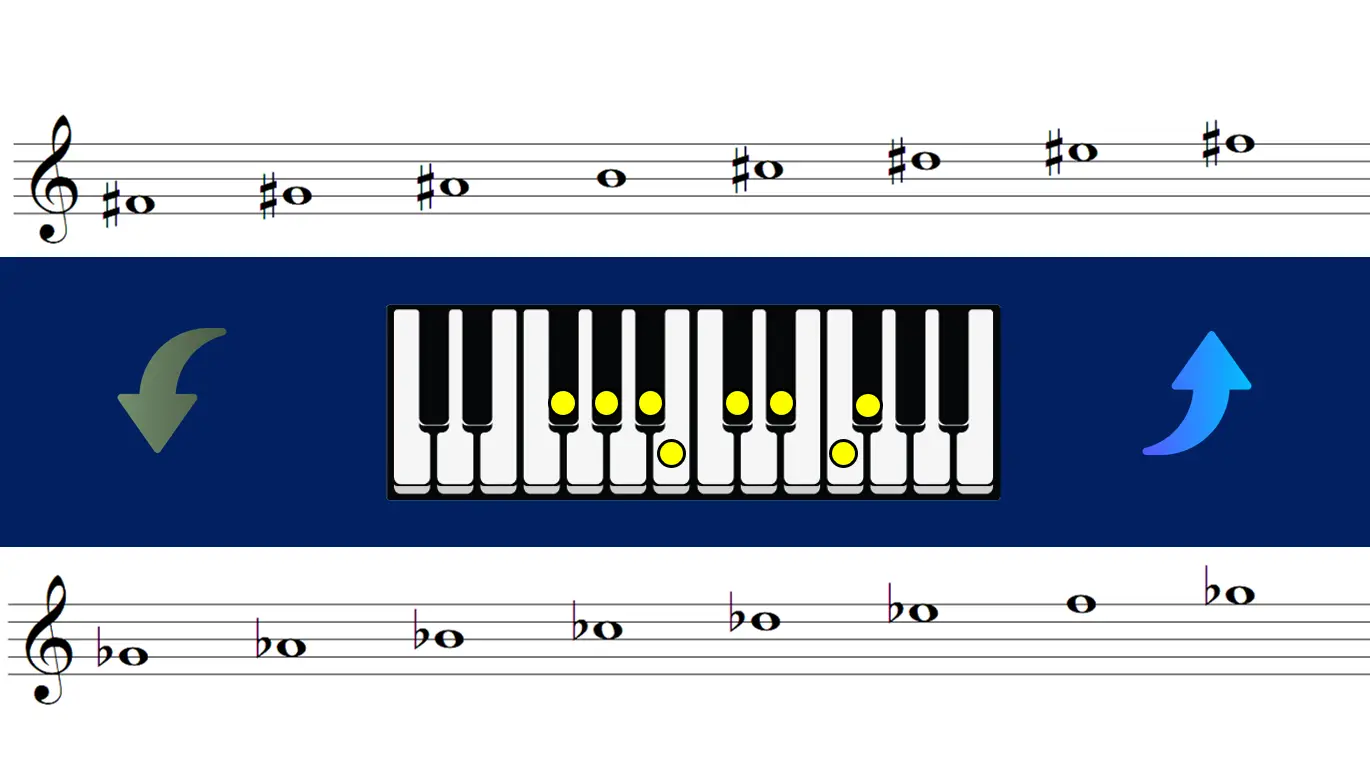
Look at them as equivalent names for those scales.
Think that once we get to seven sharps (where every note is sharpened) it actually becomes easier to think of the scale in flats.
That way it will be easier to sight read because there will be fewer accidentals.
Here goes another example for clarification:
C♯ major and D♭ major are enharmonic keys. This is, they will be identical in sound but the notes will be called and written differently in each case.
In the C♯ major scale, every degree is sharpened. So, we have 7 sharps.
But rewriting this in the key of Db Major, where only 5 flats are needed, would make this easier to sight read.
The Circle of Fifths explained
The last getaway of the post is this self-explanatory infographic of the circle of fifths.
After all, it’s said an image is worth a thousand words.

Most Recent Posts
Join the Academy
Piano Lessons
Music Theory